1、基础
适用数据:数值型。
(1)相关系数(R2)衡量
有时候,我们需要计算预测值与实际值的匹配程度,来衡量所建立模型的好坏。此时,需要计算Y、Y‘的相关系数:

其中,Cov表示协方差,Var表示方差。

(2)缩减系数
当数据的特征比样本数目还多时,此时n>m,输入的样本矩阵非满秩矩阵,在求逆时会出错。
2、线性回归
线性回归意味着将输入数据分别乘以一些常量(回归系数),相加得到输出(预测值)。
线性回归需要使用数值型数据,标称型数据需转化为二值型数据。
假设输入的预测样本为X1,为n行的列向量,W为n行的列向量,表示从样本数据得到的回归系数,则预测结果为:
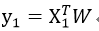
假设输入的样本数据存放在m行n列的矩阵,记为X,n个特征所决定的因变量记为Y,为m行的列向量,则需要从Y=XW得到W的值。
常用的方法为找到使得Y预测值与真实值误差最小的W,通常用平方误差衡量(该方法称为普通最小二乘法,ordinary least squares,OLS):

为了使得SE最小,我们要对SE求导,先将SE展开:
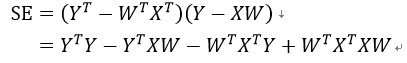
之后对W求导:
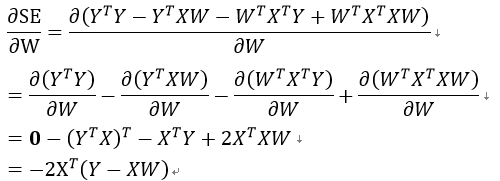
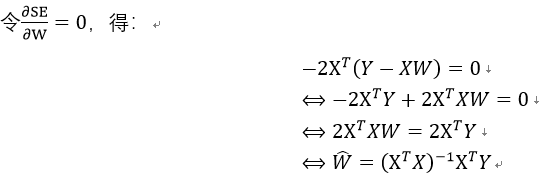
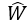 表示使得平方误差最小时的最优解。而且,此时只有在XTX存在逆矩阵时有解:
表示使得平方误差最小时的最优解。而且,此时只有在XTX存在逆矩阵时有解:
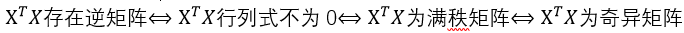
3、局部加权线性回归
线性回归易出现欠拟合现象,因为其求解的是具有最小均方误差的无偏估计。
该方法允许在估计中引入一些偏差,从而降低预测的均方误差。
局部加权线性回归(Locally Weighted Linear Regression,LWLR)中,需要给预测点附近的每个点都赋予一定的权重,然后基于最小均方误差进行普通的回归。
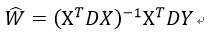
其中D是一个矩阵,用来给每个数据点赋予权重。
LWLR使用核对附近的点赋予更高的权重,常使用高斯核:
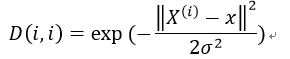
其中,X为样本矩阵,x为预测数据。
之后,通过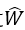 可得到预测值:
可得到预测值:

如果高斯核系数σ取1,则会达到类似最小二乘法的效果;如果过小,则会导致过拟合。
但是,LWLR最明显的缺点是增加了计算量,对每个预测数据要使用整个样本集合。
4、岭回归
岭回归是在XTX的基础上加上λI从而使得矩阵XTX非奇异,进而能够对XTX+λI求逆。
其中,矩阵I是一个m*m的单位矩阵,对角线上元素全1,其他元素全0,λ为自定义系数。
因此,回归系数的计算公式变为:
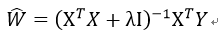
之所以称之为岭回归,是由与引入的单位矩阵中1贯穿整个对角线。形象地,在0构成的平面上有一条由1组成的“岭”。
岭回归最先用于处理特征数多于样本数的情况,但也用于在估计中加入偏差,从而使得估计结果更优,避免过拟合。
此处,引入的λ限制了所有回归系数之和,通过引入该惩罚项,会使得影响较小的特征的系数衰减到0,只保留重要的特征,该技术称为“缩减”。
为了寻找合适的λ,我们将获取的数据分为2部分:测试数据和训练数据。注意,获取的数据需要先进行标准化处理(所有特征减去均值并除以方差)通过训练数据得到回归系数,然后在测试数据测试效果。通过选择不同的 来重复这个过程,得到使得预测误差最小的λ。
如果对最小二乘法进行如下约束:
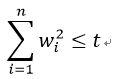
则会得到与岭回归一样的公式。
过程如下:

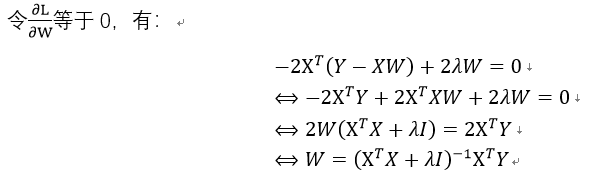
因此,岭回归也是L2范式正则化的最小二乘法。
由于岭回归限定了所有回归系数的平方和不大于t, 在使用普通最小二乘法回归的时候当两个变量具有相关性的时候,可能会使得其中一个系数是个很大正数,另一个系数是很大的负数。通过岭回归正则项的限制,可以避免这个问题。
几何意义
以两个变量为例, 普通的线性回归中,残差平方和可以表示为w1,w2的一个二次函数,是一个在三维空间中的抛物面,可以用二维(w1、w2)平面中的等值线来表示。
而限制条件w12+w22≤t则可以用圆表示:
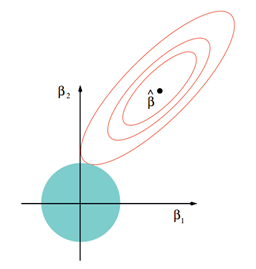
其交点则为满足条件的W。
4、lasso回归(套索算法)
Lasso(Least absolute shrinkage and selection operator)也被称为L1范式正则化的最小二乘法,是另一种缩减方法,将回归系数收缩在一定的区域内。LASSO的主要思想是构造一个一阶惩罚函数获得一个精炼的模型, 通过最终确定一些变量的系数为0进行特征筛选。
在原先的求解中,加入以下约束条件:
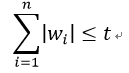
推导过程如下:
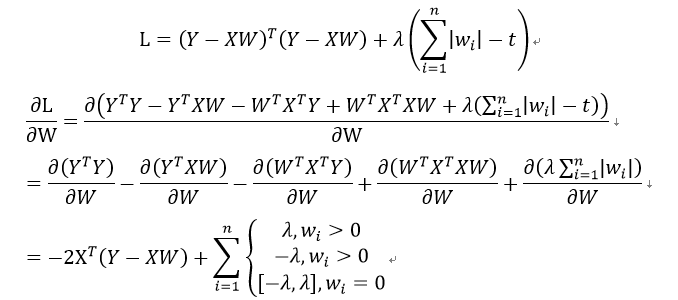
在该算法中,如果λ足够小,一些回归系数会被缩减至0,以更好地理解数据,有助于特征选择,常用于估计稀疏参数。
由于正则化项在零点处不可求导,所以使用非梯度下降法进行求解,如坐标下降法或最小角回归法。
Lasso的几何解释
同样,以两个变量为例, 普通的线性回归中,残差平方和可以表示为w1,w2的一个二次函数,是一个在三维空间中的抛物面,可以用二维(w1、w2)平面中的等值线来表示。
而限制条件|w1|+|w2|≤t则可以用正方形表示:
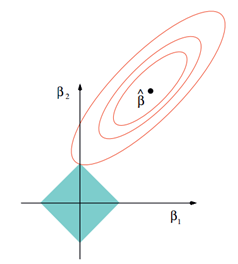
相比圆,方形的顶点更容易与抛物面相交,顶点就意味着对应的很多系数为0,而岭回归中的圆上的任意一点都很容易与抛物面相交很难得到正好等于0的系数。这也就意味着,lasso起到了很好的筛选变量的作用。
解法1:坐标轴下降法(coordinate descent)
坐标下降优化方法是一种非梯度优化算法。为了找到一个函数的局部极小值,在每次迭代中可以在当前点处沿一个坐标方向进行一维搜索。在整个过程中循环使用不同的坐标方向。一个周期的一维搜索迭代过程相当于一个梯度迭代。
与梯度下降法区别:
①梯度下降法利用目标函数的导数(梯度)来确定搜索方向的,而该梯度方向可能不与任何坐标轴平行。
②坐标轴下降法利用当前坐标系统进行搜索,不需要求目标函数的导数,只按照某一坐标方向进行搜索最小值。
坐标下降法在稀疏矩阵上的计算速度非常快,同时也是Lasso回归最快的解法。
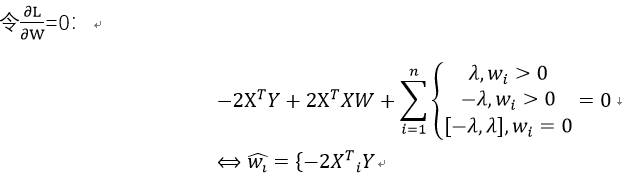
解法2:最小角回归法( Least Angle Regression)